回溯 + 剪枝
关于递归
想要了解回溯,首先要明白递归。
定义新对象或者新概念的基础规则之一是:定义中只能包含已经定义过的或含义明显的术语。因此,如果对象根据它自身来定义,就严重违反了这一规则,导致恶性循环。而另一方面,有许多编程概念根据自身定义的。此时,需要给定义加上形式约束,以保证其满足存在的唯一性,而不违反上述规则。这样的定义称为递归定义,主要用于无限集合。定义无限集合时,不可能列举出该集合的所有元素,对于一些大的有限集合也是如此。这样就需要一种更有效的方法来判断对象是否属于某个集合,而递归就是这样一种方法。
上述这段话来自《c++数据结构与算法》第四版,说的有点绕,我简单翻译一下,函数【当然函数只是一个特列,递归应该还有其他的存在】调用自身的过程中需要约束条件,这样它才会存在有限的集合,从而满足存在的唯一性。
运行时栈:每个函数(包括主函数main())的状态由以下因素决定:函数中所有局部变量的内容,函数参数的值,表明在调用函数何处重新开始的返回地址。包含所有这些信息的数据区称为活动记录或者栈框架,位于运行时栈。只要函数在执行,其活动就一直存在。这个记录时函数的私有信息池,存储了程序正确执行并正确返回到调用调用它的函数的所有信息。记录活动的寿命一般很短,因为活动记录在函数开始执行时得到动态分配的空间,在函数退出时释放其空间。
活动记录通常包含以下信息:
- 函数所有参数值
- 可以存储在其他地方的局部变量,记录活动只包含他们的描述符以及指向其存放位置的指针。
- 使得调用者重新获得控制权的返回地址,调用者指令的地址紧随这个调用之后。
- 一个指向调用程序的活动记录的指针,这是一个动态链接。【嗯。。。
- 非void 类型的函数返回值。活动记录的空间大小随调用的不同而不同,返回值放在调用程序活动记录的正上方。
上面提到,所有函数的调用,都会在运行时栈中建立活动记录。运行时栈总是反映函数当前的状态。那么递归函数也是如此。
如下图:
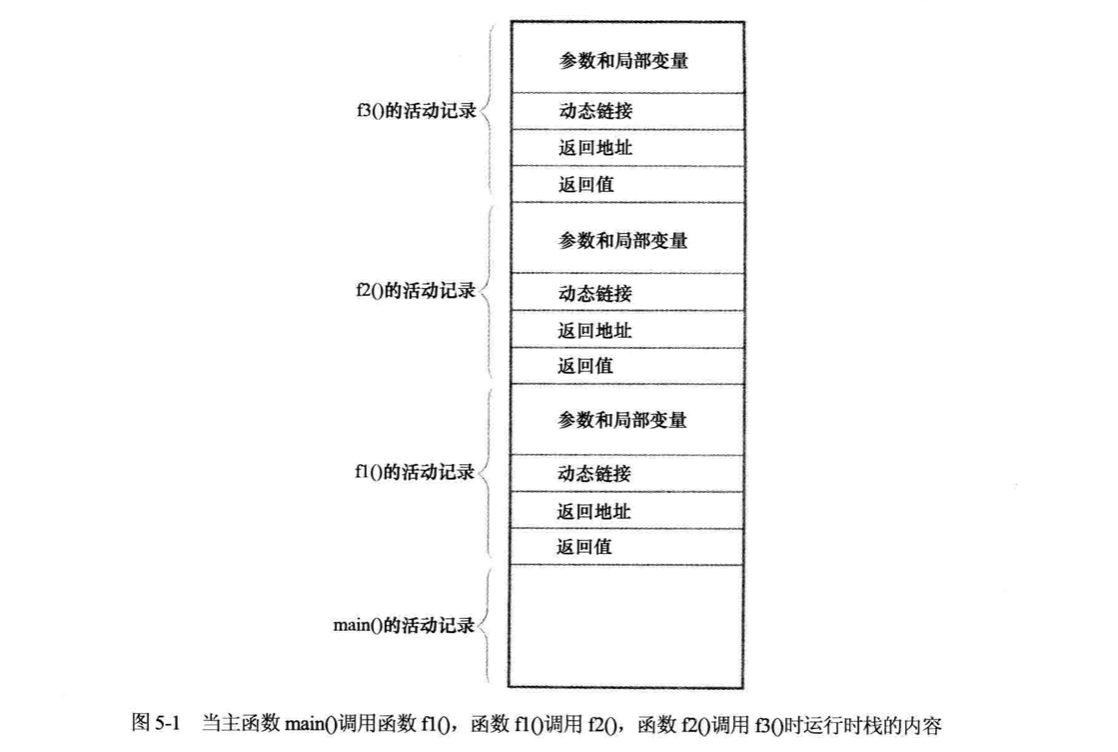
注:此时如果f3()调用了另一个函数f4(),运行时栈的空间将增大,因为函数f4()的活动记录在该栈上创建,而f3将暂停执行。如果f4()执行完成,并且后面没有调用的函数,此时会根据返回地址,可以理解为主函数执行剩下语句的地址。【使得调用者重新获得控制权的返回地址,调用者指令的地址紧随这个调用之后】,接着会执行搁置的f3,如果有返回值f3()会拿到对应的返回值,以此类推。
回溯
- 回溯算法是递归算法的一种特殊形式,回溯算法的基本思想是:对一个包括有多个结点,每个结点有若干个搜索分支的问题,把原问题分解为对若干个字问题的求解的算法;当搜索到某个结点、发现无法再继续搜索下去时,就让搜索结点回溯到该结点的前一个结点,继续搜索这个结点的其他尚未搜索过的分支;如果发现这个结点再也无法再继续搜索下去时,就让搜索过程回溯到这个结点前一个结点继续这样的搜索过程;这样的搜索过程一直进行到搜索到问题的解或搜索完了全部可搜索分支没有解存在为止。
- 深度优先搜索:顺着路径的深度去搜索,直到到达约束条件时返回,然后往深处搜索剩余的分支。
思考回溯的时候容易陷到循环里,不过可以通过画搜索树使其更直观,【怎么说呢,我还没看《开端》的大结局..】
【计算机能够回到过去,人却不能。。如果时光也可以倒流,是不是会少些遗憾呢 啊啊】

说多了。。下面直接看题:
78 子集
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3] 输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
来源:力扣(LeetCode)
画出搜索树:
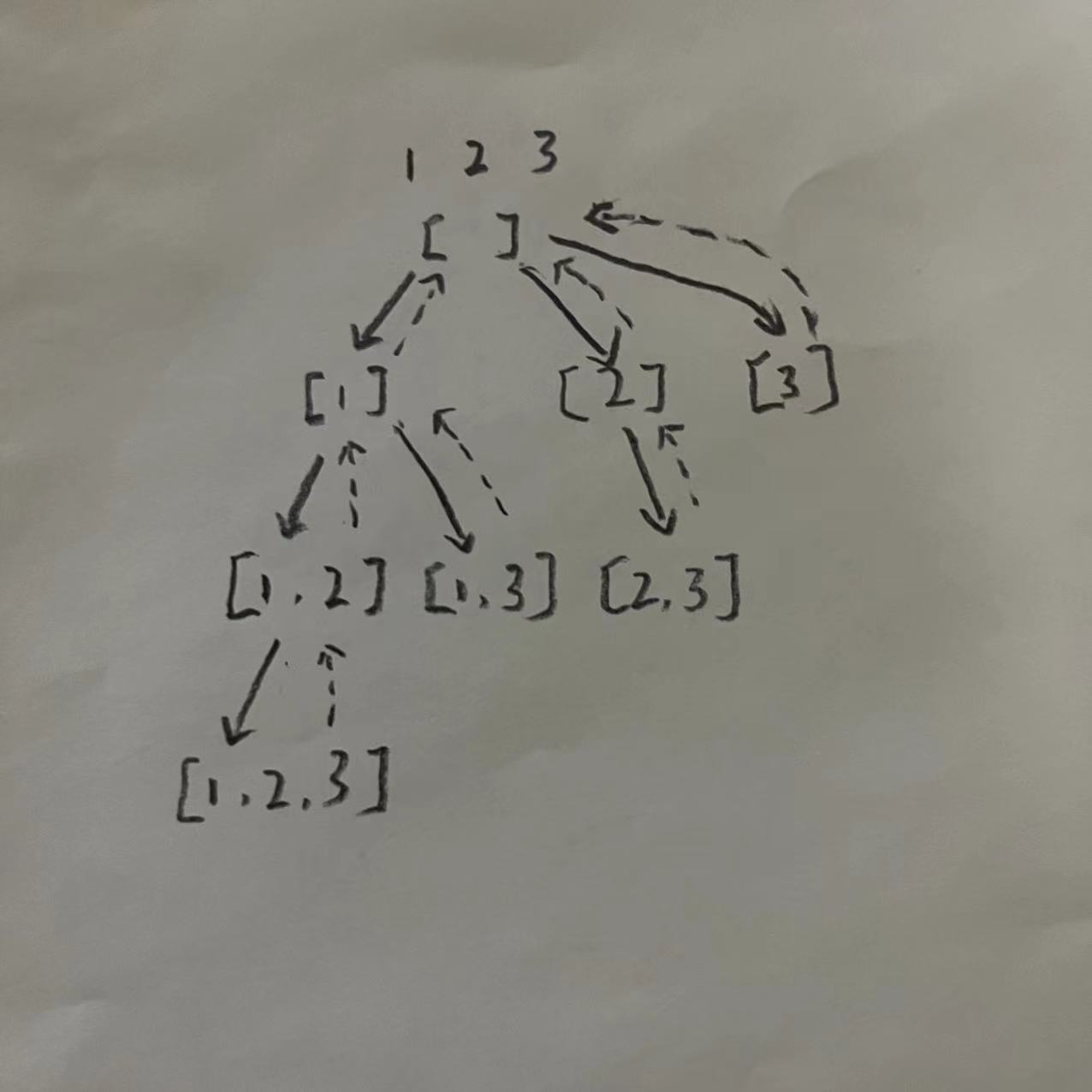
提交代码(Swift):
class Solution {
func subsets(_ nums: [Int]) -> [[Int]] {
var res = Array<[Int]>.init();
var path = Array<Int>.init();
dfs_subsets(0, nums, &res, &path);
return res;
}
func dfs_subsets(_ begin: Int, _ nums: [Int], _ res: inout [[Int]], _ path: inout [Int] ) -> Void {
let temp = path;
res.append(temp);
if temp.count == nums.count { // 这里是搜索到最深处返回
return;
}
if begin > nums.count - 1 {
return;
}
for i in begin...nums.count - 1 {
path.append(nums[i]);
dfs_subsets(i + 1, nums, &res, &path);
path.removeLast();
}
}
}
回溯 + 剪枝
- 剪枝:当确定当前结点之后分支不是我们需要的解,可以加入判断条件,避免对子分支的搜索,从而实现优化算法时空复杂度。
40.组合总和 II
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意:解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8, 输出: [ [1,1,6], [1,2,5], [1,7], [2,6] ] 示例 2:
输入: candidates = [2,5,2,1,2], target = 5, 输出: [ [1,2,2], [5] ]
- 读题可以知道,数组中字每个组合只能使用一次。那么相同的数字就可能被多次使用,为了避免这种情况可以通过排序实现去重。
- 排序也能帮助我们更好的剪枝
搜索树:
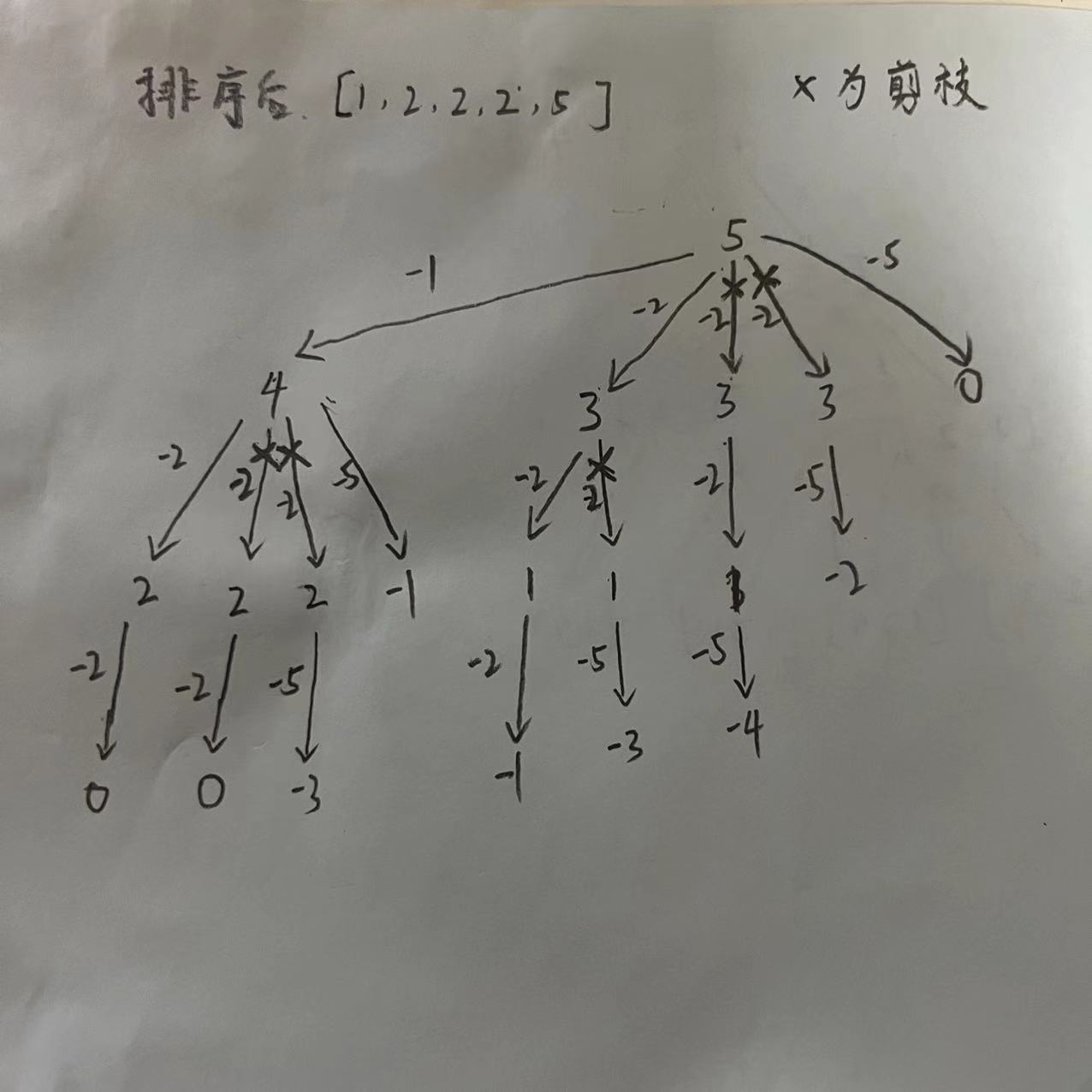
代码:
class Solution {
func combinationSum2(_ candidates: [Int], _ target: Int) -> [[Int]] {
var arr = candidates;
var res = Array<[Int]>.init();
var path = Array<Int>.init();
arr.sort();
dfs_sum_o(0,target,&used,&arr,&res,&path);
return res;
}
func dfs_sum_o(_ begin: Int, _ target: Int, _ candidates: inout Array<Int>, _ res : inout Array<[Int]>, _ path: inout Array<Int>) {
if target == 0 {
let temp = path;
res.append(temp);
return;
}
if begin > candidates.count - 1 {
return;
}
for i in begin...candidates.count - 1 {
if target - candidates[i] < 0 { // 剪枝 ,因为后面的都会小于0 直接跳过这个分支
break;
}
if i > 0 && candidates[i] == candidates[i - 1] && i > begin {// 剪枝,去重
continue;
}
path.append(candidates[i]);
dfs_sum_o(i + 1, target - candidates[i], &candidates, &res, &path);
path.removeLast();
}
}
}
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/combination-sum-ii