当你在思考状的时候你在思考什么?
在宏观世界层面(经典力学、相对论)状态可以说是确定的 deterministic
在微观世界层面(量子力学)还是确定的吗? non-deterministic
真的很神奇
有穷自动机
- 有穷自动机(FA)是由两位神经科物理科学家MeCaloch和Pitts于1948年提出,是对一类处理系统建立的数学模型。
- 这类系统具有一系列离散的输入输出信息和有穷数目的内部状态 (状态:概括了对过去输入信息的处理状况)
- 系统只需要根据当前所处状态和当前面临的输入信息就可以决定系统后继行为。每当系统处理了当前输入后,系统的内部状态也将发生改变。
FA的分类
- 确定有穷自动机(DFA)
- 非确定有穷自动机(NFA)
DFA
M = (S, Σ, δ, s0, F)
- S: 有穷状态集
-
Σ:输入字母表,输入符号集合。假设ε不是在Σ中的元素
- δ:将 S × Σ映射到S的转换函数。∀s ∈ S, a ∈ Σ, δ(s,a)表示从状态s出发,沿着标记为a的边所能到达的状态。
- s0:开始状态(或初始状态), s0∈ S
- F: 接收状态(或终止状态)集合,F ⊆S
一个例子:r =(a|b)*abb,即识别一个abb结尾的ab串。
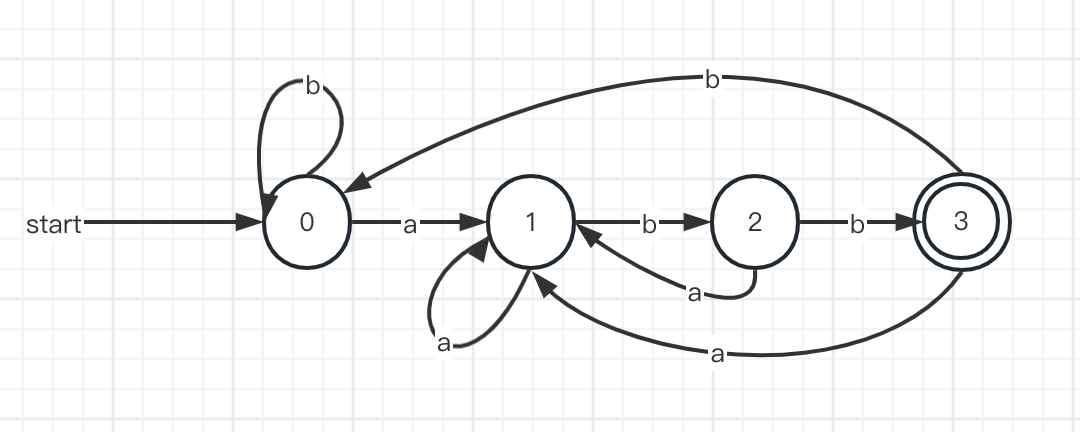
代码实现
enum State: Int{
case STATE_BEGIN = 0
case STATE_ONE = 1
case STATE_TWO = 2
case STATE_THREE = 3
case STATE_NONE
}
enum CharType {
case C_TYPE_A
case C_TYPE_B
case C_TYPE_ILLEGAL
}
func checkStr(_ str: String) -> Bool {
var state:State = .STATE_BEGIN
for c in str {
state = stateMove(getCharType(c), state)
if state == .STATE_NONE {
return false
}
}
if state == .STATE_THREE {
return true
}
return false
}
func getCharType(_ c: Character) -> CharType {
if c == "a" {
return .C_TYPE_A
}
if c == "b" {
return .C_TYPE_B
}
return .C_TYPE_ILLEGAL
}
func stateMove(_ chareType: CharType, _ state: State) -> State {
var map = [State:[CharType:State]]()
map[.STATE_BEGIN] = [.C_TYPE_A: .STATE_ONE, .C_TYPE_B: .STATE_BEGIN]
map[.STATE_ONE] = [.C_TYPE_A: .STATE_ONE, .C_TYPE_B: .STATE_TWO]
map[.STATE_TWO] = [.C_TYPE_A: .STATE_ONE, .C_TYPE_B: .STATE_THREE]
map[.STATE_THREE] = [.C_TYPE_A: .STATE_ONE, .C_TYPE_B: .STATE_BEGIN]
if let dic = map[state] {
return dic[chareType] ?? .STATE_NONE
}
return .STATE_NONE
}
NFA
M = (S, Σ, δ, s0, F)
- S: 有穷状态集
-
Σ:输入字母表,输入符号集合。假设ε不是在Σ中的元素
- δ:将 S × Σ映射到2^s的转换函数。∀s ∈ S, a ∈ Σ, δ(s,a)表示从状态s出发,沿着标记为a的边所能到达的状态。
- s0:开始状态(或初始状态), s0∈ S
- F: 接收状态(或终止状态)集合,F ⊆S
跟DFA的唯一区别是:从状态s出发沿着标记为a的边到达的状态可能有多个,并不是唯一确定的,所以叫NFA。
比如下图,在初始状态0,接收符号a,可以进入状态0或者状体1。
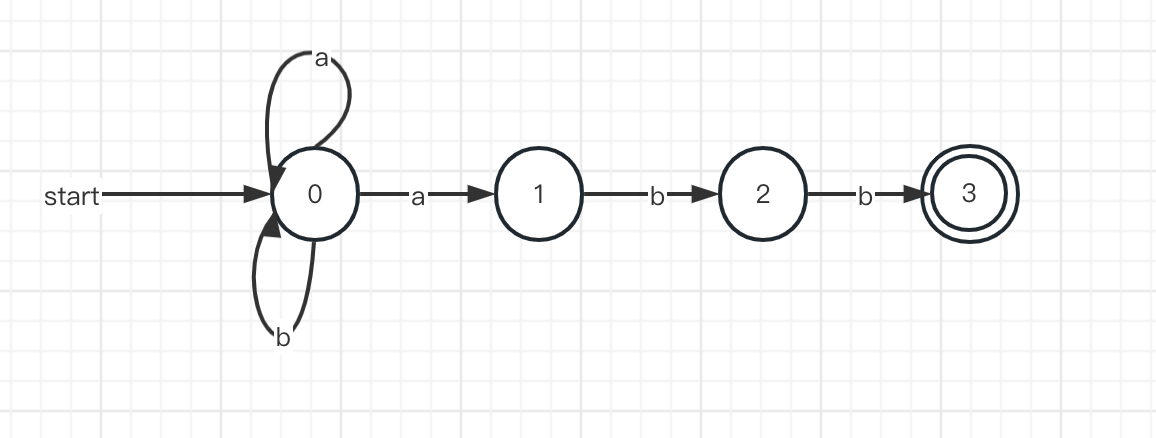
DFA和NFA具有等价性质
- 对任何NFA,存在识别同一语言的DFA
- 对任何DFA,存在识别同一语言的NFA
比如上面举例的两个图是等价的:都表示识别一个abb结尾的ab串。
DFA比NFA翻译成代码更简单,NFA比DFA更能直观表达动态机的含义。
正则表达是和FA也是等价的:r = (a|b)*abb 正则文法 ⇔ 正则表达式 ⇔ FA